>	restart:#"m02_p02"

Si se sabe que el valor de un total de 100 monedas mezcladas, de 1, 5 y 25 ptas es de 500 ptas,  ¿cuál es la distribución más probable?.

Datos:

>	dat:=[N=3,V[1]=1,V[2]=5,V[3]=25,n=100,s=500]:

>	eqN:=1=Sum(p[i],'i'=1..N);eqS:=S=-k*Sum(p[i]*ln(p[i]),i=1..N);eqSum:=s/n=Sum(V[i]*p[i],'i'=1..N);

>	Phi:=rhs(eqS)+alpha*rhs(eqN)+beta*rhs(eqSum);eqS_:=simplify(subs(dat,S=-k*sum(p[i]*ln(p[i]),i=1..N)));eqSol[i]:=Diff('Phi',p[i])=0;eqSol[i]:=diff(-k*p[i]*ln(p[i])+alpha*p[i]+beta*V[i]*p[i],p[i])=0;eqSol[i]:=p[i]=solve(eqSol[i],p[i]);

>

N:=subs(dat,N);eqN_:=1=subs(dat,sum(subs(eqSol[i],p[i]),i=1..N));eqSum_:=s/n=subs(dat,sum(subs(eqSol[i],V[i]*p[i]),i=1..N));sol:=solve(subs(dat,dat,{eqN_,eqSum_}),{alpha,beta}):alpha:=evalf(allvalues(subs(sol,alpha/k)*k))[1];beta:=evalf(allvalues(subs(sol,beta/k)*k))[1];sol2:=subs(eqSol[i],p[i]):sol2_:=evalf(subs(dat,[seq(p[i]=sol2,i=1..N)]));

es decir, lo más probable es que haya en torno a 51 de 1 Pta, 39 de 5 Pta y 10 de 25 Pta, que para que verifique el enunciado elegimos 10 de 25, 40 de 5 y 50 de 1.

>	(10+40+50)*monedas,(10*25+40*5+50*1)*Pta;

Otro procedimiento:

>	restart:N:=3:val1:=1;val2:=5;val3:=25;eq1:=n1+n2+n3=100;eq2:=n1*val1+n2*val2+n3*val3=500;isolve({eq1,eq2});assign(%):

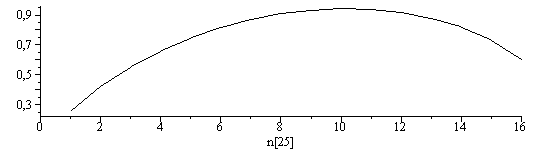
>	for _Z1 from iquo(100,6) by -1 to 1 do S(_Z1):=sum('-n||i'*ln('n||i'/100)/100,'i'=1..N):print(_Z1,n1,n2,n3,n1+n2+n3,n1*val1+n2*val2+n3*val3,evalf(S(_Z1))); od:

>	plot([seq([i,S(i)],i=0..16)],'n[25]'=0..16,colour=black);

>