>	restart:#"m01_p44"

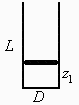
En un cilindro vertical de 10 cm de diámetro y 50 cm de altura, cerrado por abajo, hay una especie de émbolo  de 5 kg, inicialmente anclado al cilindro, encerrando un volumen de 1 L de aire a 300 kPa, todo ello en presencia de la atmósfera normal. En un cierto instante queda liberado el émbolo. Suponiendo que el movimiento es con fricción despreciable, se pide:
a) Plantear la ecuación del movimiento del émbolo y determinar la aceleración inicial.
b) Evolución que sufre el gas encerrado durante la expansión, determinando la presión justo antes de que el émbolo escape del cilindro.
c) Plantear el balance energético del émbolo desde el instante inicial hasta que abandona el cilindro.
d) Calcular la velocidad de salida.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Aire":dat:=[D=0.1*m_,L=0.5*m_,mE=5*kg_,V1=1e-3*m_^3,p1=300e3*Pa_];

Eqs. const.:

>	dat:=op(dat),get_gas_data(su),Const,SI2,SI1:

a) Plantear la ecuación del movimiento del émbolo y determinar la aceleración inicial.

>	eqBF:=mE*diff(z(t),t,t)=(p-p0)*A-mE*g;a0:=(p1-p0)*A/mE-g;A=Pi*D^2/4;A_:=evalf(subs(dat,rhs(%)));a0_:=evalf(subs(A=A_,dat,a0));

i.e. unos 300 m/s2.

b) Evolución que sufre el gas encerrado, durante la expansión.

isoentrópica, ya que es adiabática (por ser rápida) y sin fricción, i.e.

>	eqG:=p*V^gamma=cte;eqG:=p*z^gamma=p1*z1^gamma;p2:=p1*(z1/L)^gamma;z1:=V1/'A';z1_:=evalf(subs(A=A_,dat,%));p2_:=subs(dat,evalf(subs(A=A_,dat,p2),3));

i.e. el émbolo estaba inicialmente a 0,13 m del fondo (y a 300 kPa), y cuando sale (con x2=0,5 m) había 44 kPa en el interior (luego, tiene lugar un proceso de expansión brusca, que se estudia en mecánica de fluidos).

c) Plantear el balance energético del émbolo desde el instante inicial hasta que abandona el cilindro.

>	eqBE:=DE=Q+W;eqBE:=mE*diff(z(t),t)^2/2+mE*g*(z-z1)=Int((p-p0)*'A',z='z1'..z);

También se puede obtener integrando la ecuación del movimiento en dz y trasponiendo el término gravitatorio.

La integral es:

>	eqW:=Int((p-p0)*A,z='z1'..z)=Int((p1*'z1'^gamma/z^gamma-p0)*A,z='z1'..z);eqW:=Int((p-p0)*A,z='z1'..z)=int((p1*z1^gamma/z^gamma-p0)*A,z=z1..z);

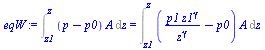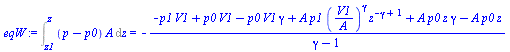d) Calcular la velocidad de salida.

El balance energético del émbolo entre el estado inicial (1) y el de salida (2) queda:

>	eqBE:=mE*v2^2/2+mE*g*(L-'z1')=collect(subs(z=L,rhs(eqW)),{p0,V0});subs(A=A_,dat,SI0,evalf(subs(dat,eqBE)));v2_:=solve(subs(SI0,%),v2)[1]*(m_/s_);

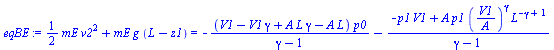i.e. el émbolo sale a 1,4 m/s.

>