>	restart:#"m01_p41"

Se tiene un cilindro vertical de 1 cm de diámetro y 20 cm de altura, abierto por abajo, amarrado a un soporte y con un émbolo de 0,1 kg cuya cara superior está a 10 cm del fondo del cilindro, encerrando una cierta cantidad de aire. Se pide:
a) Presión y cantidad de gas atrapado.
b) Trabajo mínimo necesario para obligar a que la cara interior del émbolo quede a 15 cm del fondo.
c) Masa de la pesa que habría que colgar del émbolo para que en el equilibrio final quedase como se ha dicho en el punto anterior.
d) Hacer un esquema de la evolución del émbolo si al colocar la pesa se suelta bruscamente y determinar alrededor de qué posición oscilaría.
e) Punto más bajo que alcanzaría el émbolo en el caso anterior.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):assume(x1>0,x2>0,x3>0);

>	su1:="Aire":su2:="Laton":dat:=[A=evalf(Pi*(0.01*m_)^2/4),L=0.2*m_,mE=0.1*kg_,z1=0.1*m_,z2=0.15*m_];

Esquema:

>

>

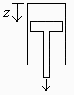
Ecs. const.:

>	eqET:=eq1_14;eqBE:=eq1_5;eqEE:=eq1_16;gdat:=get_gas_data(su1):sdat:=get_sol_data(su2):dat:=op(dat),Const,gdat,SI2,SI1:

a) Presión y cantidad de gas atrapado.

>	eqBF:=mE*diff(z(t),t,t)=(p-p0)*A+mE*g-Ff;eqBEmec:=int(mE*diff(z(t),t,t)*diff(z(t),t),t)=Int((p-p0)*A+mE*g-Ff,z);T1:=T0:eqBF1:=0=(p1-p0)*A+mE*g;p1_:=p0-mE*g/A;p1_:=subs(dat,%);eqeT:=m=p1*A*z1/(R*T0);eqET_:=subs(p1=p1_,dat,%);eqET__:=n=subs(%,dat,m/M);

i.e., la presión del gas atrapado inicialmente sería de 87,5 kPa, habiendo encerrado 0.29 mmol de aire.

b) Trabajo mínimo necesario para obligar a que la cara interior del émbolo quede a 40 cm del fondo.

Para minimizar el trabajo, conviene hacer el proceso lentamente (isotérmicamente) para minimizar la fricción y el calentamiento. Sea F la fuerza necesaria.

>

eqBF_lento:=0=(p-p0)*A+mE*g-Ff+F;Ff:=0;F_:=solve(%,F):WF:=Int(F,z=z1..z2);eqET;eq_process:=p*V=p1*V1;eq_process:=p*x=p1*x1;p2=p1*z1/z2;p2_:=subs(dat,p1_*z1/z2);WF:=int(subs(p=p1*z1/z,F_),z=z1..z2);WF:=-A*p1*z1*ln(z2/z1)+A*p0*(z2-z1)-mE*g*(z2-z1)+Ff*(z2-z1);WF_:=subs(dat,evalf(subs(p1=p1_,dat,WF)));WFterms:=[-A*p1*z1*ln(z2/z1),+A*p0*(z2-z1),-mE*g*(z2-z1)];WFterms_:=subs(dat,evalf(subs(p1=p1_,dat,WFterms)));

i.e., hay que hacer 0,06 J de trabajo, resultado de recibir 0,05 J por descenso del peso del émbolo, de hacer 0,39 J contra la atmósfera, y de recibir 0,28 J del gas encerrado.

El gas atrapado da 0,28 J de trabajo y toma 0,28 J de calor en el proceso, pero globalmente ni toma ni da energía.

NOTA AL MARGEN. Al estudiar la exergía, se vería que el trabajo mínimo para realizar un proceso con un sistema en presencia de una atmósfera infinita es Wmin=DE+p0*DV-T0*DS. Para nuestro caso, aplicándolo al gas atrapado:

>	Wmin=DPhi;Wmin=DE+p0*DV-T0*DS;T2=T1;DE:=0;DV:=A*(z2-z1);p0DV_:=subs(dat,p0*DV):'p0*DV'=evalf(%,3);DS:=m*(c[p]*ln(T2/T1)-R*ln(p2/p1));T0DS_:=subs(dat,evalf(subs(eqET_,p1=p1_,p2=p2_,T2=T1,dat,T0*DS))):'-T0*DS'=-evalf(%,3);Wmin_:=DE+p0DV_-T0DS_:'Wmin'=evalf(%,2);

i.e., el trabajo mínimo para obligar al gas a realizar ese proceso es de 0,11 J (que con los 0,28 J que proporciona el propio gas son los 0,39 J que pasan al ambiente). Pero en el problema presente, parte de ese trabajo lo haría el campo gravitatorio (los 0,05 J de bajada de los 0,1 kg), con lo cual se obtiene el resultado anterior: 0,11-0,05=0,06 J.

c) Masa de la pesa que habría que colgar del émbolo para que en el equilibrio quedase como se ha dicho en el punto anterior, y variación de energía de la pesa, y punto más bajo que alcanzaría la pesa si al colocarla se suelta bruscamente.

Aplicando el balance de fuerzas integrado al conjunto émbolo+pesa, y sabiendo que la velocidad será nula en el estado inicial y en el de máxima elongación, y que ahora el proceso será rápido y para el aire se podrá aproximar como isoentrópico, tendremos:

>

eqBF_final:=0=(p2-p0)*A+mE*g-Ff+F;F:=mP*g;mP_:=subs(Ff=0,p2=p2_,dat,solve(eqBF_final,mP));eqBF:=(mE+mP)*diff(z(t),t,t)=(p-p0)*A+(mE+mP)*g-Ff;eqBFint:=int((mE+mP)*diff(z(t),t,t)*diff(z(t),t),t)=Int((p-p0)*A+(mE+mP)*g-Ff,z=z1..z3);eqBFint:=0=Int((p1*z1^gamma/z^gamma-p0)*A+(mE+mP)*g-Ff,z=z1..z3);eqBFint_:=subs(p1=p1_,mP=mP_,dat,SI0,value(eqBFint)):evalf(%,2);z3_:=fsolve(eqBFint_,z3=0.11..0.3)*m_;plot(rhs(eqBFint_),z3=.01..0.25,eq=-0.1..0.1);eq14:=p*z^gamma=cte;z4:=z1*(p1/p4)^(1/gamma);p4:=p2;z4_:=subs(p1=p1_,p2=p2_,dat,z4);

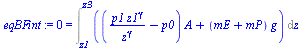i.e., la pesa ha de ser de 0,23 kg, y la cara superior del émbolo bajaría hasta 0,18 m (i.e. no llega a salirse), oscilando alrededor de 0,13 m.

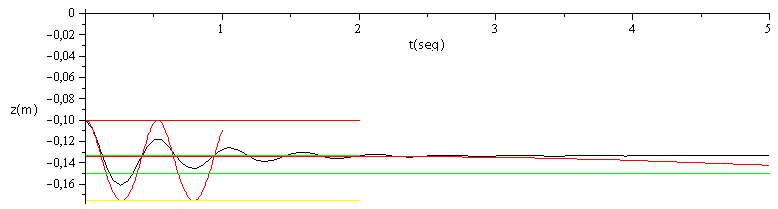
Si suponemos un coeficiente de amortiguamiento viscoso apropiado, podríamos tener un gráfico bastante realista de la evolución. Se ha añadido también una función de atemperamiento, pero no muy realisata, porque los tiempos de relajación térmica son siempre mucho mayores que los de equilibrado mecánico.

>

with(plots):mEP:=mE+mP;mEP:=subs(mP=mP_,dat,%);deq1:=diff(z(t),t)=zp(t):deq2:='mEP'*diff(zp(t),t)='mEP'*g+(p-p0)*A-coef*zp(t);ic1:=z(0)=z1;ic2:=zp(0)=0;eqs:=subs(dat,SI0,{deq1,subs(p=p1_*(z1/z(t))^gamma,deq2),ic1,ic2});dsol1:=dsolve(subs(coef=1,eqs),{z(t),zp(t)},numeric):pl0:=odeplot(dsol1,[t,-z(t)],0..5,numpoints=100,labels=["t(seg)","z(m)"],colour=black):dsol9:=dsolve(subs(coef=0,eqs),{z(t),zp(t)},numeric):pl9:=odeplot(dsol9,[t,-z(t)],0..1,numpoints=100,labels=["t(seg)","z(m)"]):pl1:=plot({[[0,0],[2,0]],[[0,-subs(SI0,z4_)],[2,-subs(SI0,z4_)]],[[0,-subs(SI0,z3_)],[2,-subs(SI0,z3_)]]}):pl2:=plot({[[0,0],[2,0]],[[0,-subs(dat,SI0,z1)],[2,-subs(dat,SI0,z1)]],[[0,-subs(dat,SI0,z2)],[5,-subs(dat,SI0,z2)]]}):pl3:=plot(0.05*piecewise(x>2,exp(-((x-2)/7)^2)-1,0)-0.134,x=0..5):display(pl0,pl9,pl1,pl2,pl3);

Warning, the name changecoords has been redefined

>