>	restart:#"m01_p36"

Dentro de un cilindro vertical de 25 cm de diámetro hay dióxido de carbono limitado superiormente por un émbolo que mantiene la presión interior en 120 kPa. Inicialmente el émbolo está a 0,5 m de altura sobre el fondo del cilindro, y el gas a 15 ºC. Entonces se conecta a 220 V una resistencia eléctrica en el interior, observándose que al cabo de 3 minutos el volumen ha aumentado un 50%. Suponiendo que se puedan despreciar las pérdidas de calor por las paredes y la fricción del émbolo, se pide:
a) Plantear el balance energético del gas, y de la resistencia eléctrica.
b) Temperatura final del gas.
c) Trabajo que realiza o recibe el gas.
d) Valor numérico de cada término del balance energético del gas, y de la resistencia eléctrica.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="CO2":dat:=[D=0.25*m_,p1=120e3*Pa_,z1=0.5*m_,Vele=220*V_,tele=3*60*s_,V2=1.5*V1];A_:=evalf(subs(dat,Pi*D^2/4));V1:=A*z1;V1_:=evalf(subs(dat,A_*z1));

Esquema:

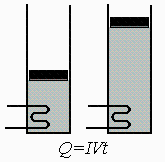
Ecs. const.:

>	eq1_5;eqET:=eq1_14;eq1_16;dat:=op(dat),get_gas_data(su1),get_liq_data(su1),Const,SI2,SI1:get_pv_data(su1):

a) Plantear el balance energético del gas, y de la resistencia eléctrica.

>	eqBEgas:=m*c[v]*(T2-T1)=Q+W;eqQgas:=Q=(Vele^2/Rele)*tele;eqWgas:=W=-Int(p,V=V1..V2);eqBEres:=m[res]*c*DT[res]=Q[res]+W[res];eqBEres:=0=-Qele+Vele*Iele*tele;

i.e. el gas recibe calor de la resistencia, y parte lo emplea en dar trabajo y el resto en incrementar su energía interna (calentarse).

En cuanto a la resistencia eléctrica, consideraremos que todo el trabajo eléctrico que recibe lo da al gas en forma de calor, despreciando la parte de energía que se almacena en ella.

b) Temperatura final del gas.

>	eqET12:=p1*V1/T1=p2*V2/T2;p2=p1;p1_:=subs(dat,p1);T1_:=subs(dat,T0);eqET12:=T2=T1*V2/V1;eqET12_:=subs(T1=T1_,dat,dat,eqET12);T2=TKC(rhs(%));

c) Trabajo que realiza o recibe el gas.

>	eqW:=Int(-p1,V=V1..V2)=subs(dat,evalf(subs(dat,A=A_,dat,int(-p1,V=V1_..V2))));eqW0:=Int(-p0,V=V1..V2)=subs(dat,evalf(subs(dat,A=A_,dat,int(-p0,V=V1_..V2))));eqEmb:=DE=mE*g*(z2-z1);mE:=(p1-p0)*A/g;mE_:=evalf(subs(dat,A=A_,%));eqEmb_:='mE*g*(z2-z1)'=subs(dat,dat,mE_*g*(V2/A-z1));

i.e., el gas realiza un trabajo de 1,47 kJ, 1,23 kJ contra el ambiente y 0,24 kJ sobre el émbolo.

Puede calcularse la variación de entropía del gas (serviría para determinar la pérdida de exergía en el proceso):

>	eqS12:=DS=m*(c[p]*ln(T2/T1)-R*ln(p2/p1));eqm:=m=p1*V1/(R*T1);eqm_:=subs(A=A_,T1=T0,dat,%);eqS12_:=subs(dat,evalf(subs(p2=p1,eqET12,eqm,dat,dat,T1=T0,A=A_,eqS12)));

d) Valor numérico de cada término del balance energético del gas, y de la resistencia eléctrica.

>	eqDU:=m*c[v]*(T2-T1)=subs(eqm,eqET12_,A=A_,dat,T1=T0,dat,m*c[v]*(T2-T1));eqW:=W=rhs(eqW);eqQ:=Q=DU-W;eqQ:=Q=rhs(eqDU)-rhs(eqW);

i.e. el gas recibe 6,5 kJ de calor, da 1,5 kJ de trabajo y almacena 5 kJ de energía. La resistencia recibe 6,5 kJ de trabajo eléctrico y los da en forma de calor.

Podemos también calcular el valor de la resistencia eléctrica.

>

eqBEgas:=Qele=DU+W;eqBEgas:=Qele[p]=DH;eqBEgas:=Qele=m*c[p]*(T2-T1);eqBEgas:=Qele=(gamma/(gamma-1))*m*R*(T2-T1);eqBEgas:=Qele=(gamma/(gamma-1))*(p2*V2-p1*'V1');eqBEgas:=Qele=(gamma/(gamma-1))*p1*(V2-'V1');eqBEres:=Qele=(Vele^2/Rele)*tele;Rele_:=solve(rhs(eqBEgas)=rhs(eqBEres),Rele);Rele__:=subs(dat,V_=sqrt(W_*Omega),A=A_,dat,%);

i.e. la resistencia ha de ser de unos 1300 ohmios, la corriente circulante I=V/R=0,165 A y la potencia disipada I^2*R=36 W, que en los 3 minutos son los 6,5 kJ antes hallados..

>