| > | restart:#"m01_p35" |
Se desea comprobar que el aire pesa y medir su densidad, para lo que se realiza el experimento siguiente. Se tiene una esfera de 2501 mm de diámetro exterior, de aluminio, con una válvula que puede conectarse a un equipo de vacío. Inicialmente, conteniendo aire a 201 ºC y 950,5 kPa, la esfera con la válvula tienen una masa de 2191 g. Después de aspirar algo de aire y esperar al atemperamiento, cuando la presión interior es 500,5 kPa la masa es 2141 g, y para 50,5 kPa 2101 g. Se pide:
a) Determinar la densidad del aire a partir de las medidas extremas, indicando la incertidumbre y comparándola con el modelo de gas ideal.
b) Indicar si el modelo de gas ideal es apropiado, y cómo se podría mejorar la exactitud experimental.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma): |
| > | su1:="Aire":su2:="Aluminio_anodizado":dat:=[D=0.25*m_,DD=1e-3*m_,T0=(20+273)*K_,DT=1*K_,p1=95e3*Pa_,Dp=500*Pa_,m1=0.219*kg_,Dm=1e-3*kg_,p2=50e3*Pa_,m2=0.214*kg_,p3=5e3*Pa_,m3=0.210*kg_]; |
Esquema:
Ecs. const.:
| > | eqET:=eq1_14;dat:=op(dat),get_gas_data(su1),Const,SI2,SI1:Sdat:=get_sol_data(su2):m_air:=evalf(subs(dat,p1*(Pi*D^3/6)/(R*T0))); |
a) Determinar la densidad del aire a partir de las medidas extremas, indicando la incertidumbre y comparándola con el modelo de gas ideal.
Supondremos que de 95 kPa a 5 kPa se extrae prácticamente todo el aire, luego su masa se obtendrá por diferencia de pesadas.
Supondremos que el volumen de aire es aproximadamente el de la esfera por fuera.
| > | eq1_11;mair:=m1-m3;Vair:=Pi*D^3/6;eq1:=rho=mair/Vair;eq1_:=evalf(subs(dat,eq1));eq1sigma:=Drho/rho='sqrt((Dm/m)^2+(DV/V)^2)';eqsm:=dm/m=Dm/(m3-m2);eqsm_:=subs(dat,%);eqsV:=DV/V=3*DD/D;eqsV_:=subs(dat,%);eq1sigma:=Drho/rho='sqrt((Dm/m)^2+(DV/V)^2)';eq1sigma_:=subs(m=m1-m3,eqsm,DV=solve(eqsV,DV),dat,%);Drho=subs(eq1_,solve(eq1sigma_,Drho));Drho_exp=0.1*kg_/m_^3;eqMGI:=rho=p/(R*T);eqMGI:=rho=subs(dat,p0/(R*T0));eqMGIsigma:=Drho/rho='sqrt((Dp/p)^2+(DT/T)^2)';eqMGIsigma_:=subs(p=p1,T=T0,dat,%);Drho_MGI=0.01*kg_/m_^3; |
i.e., la medida indica rho=1,1+/-0,1, mientras que el MGI indica rho=1,19+/-0,01.
Conclusión, la medida y el modelo son congruentes (hay punto común en el rango de valores: (1,0..1,2) y (1,18..1,20), pero la medida no parece muy precisa.
Nótese que se ha medido la densidad en las condiciones iniciales, pues bien se ve que la densidad varía con la presión (y con la temperatura).
| > |
b) Indicar si el modelo de gas ideal es apropiado, y cómo se podría mejorar la exactitud experimental.
De la comparación de densidades en el estado inicial, ya se ha dicho que el MGI es plausible en ese estado. Para ver si es también adecuado en otros estados, representamos las masas medidas con las predichas (añadiendo la tara):
| > | plot(subs(dat,SI0,[[[p1,m1-m3-Dm],[p1,m1-m3+Dm]],[[p2,m2-m3-Dm],[p2,m2-m3+Dm]],[[p3,m3-m3-Dm],[p3,m3-m3+Dm]],[[p1,m1-m3],[p2,m2-m3]],[[p2,m2-m3],[p3,m3-m3]],[[0,0],[1e5,subs(dat,SI0,1e5*Vair/(R*T0))]]]),color=black); |
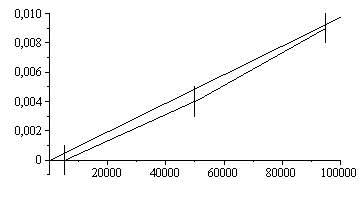 |
i.e. ambos resultados son coherentes (dentro de la incertidumbre experimental).
Se concluye, pues, que la masa variá linealmente con la presión, y que la pendiente es la apropiada (pero no se ha verificado la dependencia con la temperatura).
Para mejorar la exactitud se puede:
1. Tomar más medidas y obtener una recta de regresión.
2. Mejorar la precisión de la medida: usando básculas más precisas, mejores piezómetros, midiendo la capacidad real del aparato (si se pudiera), etc.
3. Mejorar la precisión relativa de la medida. Llenando el recipiente a alta presión, y/o trabajando a baja temperatura, habría más aire dentro y disminuiría la incertidumbre.
4. Idear otro experimento mejor: variando los parámetros del actual, sumergiendo el aparato en agua si la compensación por empuje de Arquímedes es adecuada, u otra idea mejor.
Historia. Según Aristóteles, el agua y la tierra tienen atracción 'peso', mientras que el aire y el fuego tienen repulsión 'levitación'. Galileo fue el primero en preguntarse si el aire pesaba y tratar de medirlo (por diferencia de pesada de una botella con aire a presión y obtuvo rho=2 kg/m3.
| > |