>	restart;#"m01_pp1"

Un manómetro en U, de vidrio de 3 mm de diámetro interior y 6 mm de diámetro exterior, tiene los lados de 1 m de altura y la conexión por abajo de longitud despreciable. El tubo se ha llenado con agua hasta 600 mm de altura en cada lado, y se ha tapado una de las bocas. Se pide:
a) Determinar el efecto del cambio de presión ambiente sobre las alturas de los meniscos (dz/dpamb), particularizando para p=1 kPa.
b) Determinar el efecto del cambio de temperatura ambiente sobre las alturas de los meniscos (dz/dTamb), particularizando para T=5 ºC. Puede tomarse para el coeficiente de expansión cúbica del agua 140∙10-6 1/K y para el de expansión lineal del vidrio 9∙10-6 1/K, ambos a 20 ºC.
c) Se ha conectado la otra boca a otro sistema del que se desea medir la presión, observándose que las alturas de los meniscos se estabilizan en 834 mm y 368 mm, siendo este último el del extremo cerrado. Determinar la presión del sistema, sabiendo que la presión atmosférica es de 93 kPa y la temperatura ambiente de 25 ºC.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="H2O":su2:="Aire":dat:=[Dp=1e3*Pa_,DT=5*K_,Di=3e-3*m_,De=6e-3*m_,L=1*m_,z1_0=600e-3*m_,z2_0=600e-3*m_,z1_1=834e-3*m_,z2_1=368e-3*m_,p0=93e3*Pa_,T0=(25+273)*K_,alpha_w=140e-6/K_,alpha_g=9e-6/K_];

Esquema:

>

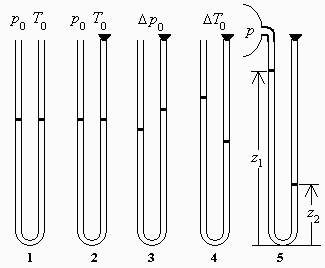
Eqs. const.:

>	Adat:=get_gas_data(su2):Wdat:=get_liq_data(su1):dat:=op(dat),Const,SI2,SI1:

a) Determinar el efecto del cambio de presión ambiente sobre las alturas de los meniscos (dz/dpamb), particularizando para p=1 kPa.

Tomamos z respecto al punto más bajo.

La variable independiente es p1, y las dependientes z1, z2, y p2.

Consideraremos que el aire atrapado no varía de composición, i.e. que la evaporación del agua en el tubo es despreciable (se necesitan muchos días para saturar el aire porque no hay convección y la difusión es muy lenta).

>

eqBF:=p1+rho*g*z1=p2+rho*g*z2;eqBMw:=z1+z2=constant;eqBMa:=m=p*V/(R*T);eqBMa:=p2*(L-z2)=constant;eqBFdif:=1+rho*g*dz1/dp1=dp2/dp1+rho*g*dz2/dp1;eqBMwdif:=dz1+dz2=0;eqBMadif:=(L-z2)*dp2/dp1-p2*dz2/dp1=0;dp2_dp1:=solve(%,dp2)/dp1:dp2/dp1=%;eqinicial:=p2=p0;eqBFdif_:=subs(dp2=dp1*dp2_dp1,dz2=-dz1,eqinicial,eqBFdif);dz1_dp1:=solve(%,dz1)/dp1:dz1/dp1=%;dz1_dp1_:=subs(Wdat,z2=z2_0,dat,dz1_dp1):dz1/dp1=evalf(1e6*subs(SI0,%),2)*mm_/kPa_;

i.e. si la presión ambiente aumenta en 1 kPa, el menisco abierto baja 4 mm (y el cerrado sube otros 4 mm).

Nótese que la diferencia de presión manométrica es de sólo 8 mm de columna de agua (80 Pa).

b) Determinar el efecto del cambio de temperatura ambiente sobre las alturas de los meniscos (dz/dTamb), particularizando para T=5 ºC. Puede tomarse para el coeficiente de expansión cúbica del agua 140∙10-6 1/K y para el de expansión lineal del vidrio 9∙10-6 1/K, ambos a 20 ºC.

La variable independiente es T, y las dependientes z1, z2, y p2, porque vamos a suponer que lo único importante es la dilatación del aire, y no la del agua ni la del vidrio.

>

eqBF:=p1+rho*g*z1=p2+rho*g*z2;eqBMw:=z1+z2=constant;eqBMa:=m=p*V/(R*T);eqBMa:=p2*(L-z2)/T=constant;eqBFdif:=0+rho*g*dz1/dT=dp2/dT+rho*g*dz2/dT;eqBMwdif:=dz1+dz2=0;eqBMadif:=(dp2/dT)*(L-z2)/T-p2*(L-z2)/T^2-(p2/T)*dz2/dT=0;dp2_dT:=solve(%,dp2)/dT;eqBFdif_:=subs(dp2=dT*dp2_dT,dz2=-dz1,eqBFdif);dz1_dT:=solve(%,dz1)/dT;eqinicial:={p2=p0,T=T0};dz1_dT_:=subs(Wdat,z2=z2_0,eqinicial,dat,dz1_dT):dz1/dT=evalf(1e3*subs(SI0,%),2)*mm_/K_;

i.e. si la temperatura ambiente aumenta en 5 ºC, el menisco abierto sube 6 mm (y el cerrado baja otros 6 mm).

Puede comprobarse que la dilatación del agua y del vidrio no cuentan, de la manera siguiente.

Si sólo dilata el agua y no el vidrio, una columna de 0,6 m dilataría Dz=z*alpha*DT=600*140e-6*5=0,42 mm.

Si dilata el vidrio también, la dilatación aparente del agua será menor. Como sólo influye el aumento de sección, pero no el de altura del tubo de vidrio, la dilatación aparente será Dz=z*(alpha_w-2*alpha_g)*DT=600*(140-2*9)1e-6*5=0,37 mm.

>	Dz_w:=z1_0*alpha_w*DT;Dz_w_:=subs(dat,Dz_w):'Dz_w'=evalf(%,2);Dz_wg:=z1_0*(alpha_w-2*alpha_g)*DT;Dz_wg_:=subs(dat,Dz_wg):'Dz_wg'=evalf(%,2);

c) Se ha conectado la otra boca a otro sistema del que se desea medir la presión, observándose que las alturas de los meniscos se estabilizan en 834 mm y 368 mm, siendo este último el del extremo cerrado. Determinar la presión del sistema, sabiendo que la presión atmosférica es de 93 kPa y la temperatura ambiente de 25 ºC.

Supondremos que no han variado las condiciones ambiente entre el llenado y la medida, pues, como se ha visto, influyen bastante.

Hay que resolver la variable intermedia p2.

>	eqBF:=p1+rho*g*z1_1=p2+rho*g*z2_1;eqBMw:=z1_1+z2_1=z1_0+z2_0;eqBMa:=m=p*V/(R*T);eqBMa:=p2*(L-z2_1)=p0*(L-z2_0);eqBF_:=subs(p2=solve(%,p2),eqBF);p1_:=subs(Wdat,dat,solve(%,p1)):'p1'=evalf(%,3);

i.e. la presión del sistema conectado es de 54,3 kPa.

Hay que comentar que parece no verificarse el balance másico de agua con la precisión supuesta, 1 mm. La explicación puede ser que la discrepancia es de 2 mm en la función f=z1_1+z2_1-z1_0-z2_0, cuya incertidumbre es doble de la de una simple altura: sigmaf=sqrt(4*sigmaz^2)=2sigmaz.

>	eqBMw_:=subs(dat,eqBMw);

>