>	restart;#"m01_p30"

Los antiguos fluidos refrigerantes como el R12 (diclorodifluorometano) han sido substituidos desde 1995 por otros que no destruyen la capa de ozono estratosférica, como el R134a (1,1,1,2-tetrafluoroetano). Para comprobar si una muestra de refrigerante es de R134a se ha realizado el experimento siguiente: en un dispositivo cilindro-émbolo de 3 cm de diámetro se ha dispuesto una muestra gaseosa que, a presión y temperatura ambientes, ocupa 0,3 m del cilindro; entonces se comprime rápidamente hasta que el volumen es la mitad y se miden las variaciones de presión y temperatura interiores, que resultan  p=123 kPa y  T= 30 K. Se pide:
a) Explicar el balance energético del proceso.
b) Determinar el coeficiente isoentrópico del gas.
c) Analizar la posible redundancia de los datos.
d) Determinar las capacidades térmicas molares del gas (a presión y a temperatura constantes).

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="CCl2F2":su2:="CF3CH2F":dat:=[D=3e-2*m_,x1=0.3*m_,x2=0.15*m_,Dp=123e3*Pa_,DT=30*K_]:A_:=evalf(subs(dat,Pi*D^2/4)):dat:=[op(dat),A=A_]:evalf(%,2);

Esquema:

>

>

Eqs. const.:

>	eqETg:=subs(eq1_11,eq1_12);eqEE:=eq1_16;g1dat:=get_gas_data(su1):g2dat:=get_gas_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Explicar el balance energético del proceso.

>	DE=W+Q;DE:=DU;DU:=m*c[v]*(T2-T1);W=Int(-p*A,x=x1..x2);eq12:=p1*x1^gamma=p*x^gamma;W_:=A*Int(-p0*(x1/x)^gamma,x=x1..x2);W__:=value(W_);

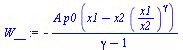Al ser el proceso rápido no dará tiempo a la transmisión de calor (i.e. Q=0), y por la geometría no habrá apenas fricción dentro del gas (i.e. Emdf=0), luego se trata de una compresión isoentrópica: el trabajo que recibe el gas (Int(-pdV)) se invierte en aumentar la energía interna térmica (DU).

b) Determinar el coeficiente isoentrópico del gas

>	gamma_:=ln(p2/p1)/ln(x1/x2);gamma__:=subs(dat,evalf(subs(p1=p0,p2=p0+Dp,dat,gamma_))):'gamma'=evalf(%,3);gamma[R12]=evalf(subs(g1dat,gamma),3);gamma[R134a]=evalf(subs(g2dat,gamma),3);

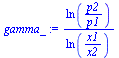i.e. parece tratarse del R134a.

c) Analizar la posible redundancia de los dato

Sí, hay un dato redundante, ya que pV/T=cte. Hemos usado Dp; si ahora usamos DT:

>	eq12_:=T1*x1^(gamma-1)=T2*x2^(gamma-1);gamma_:=1+ln((T0+DT)/T0)/ln(x1/x2);gamma__:=subs(dat,evalf(subs(dat,gamma_))):'gamma'=evalf(%,3);

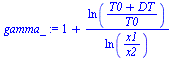¡Vaya!, ahora parece tratarse del R12.

CONCLUSIÓN: Como era de suponer a la luz de otros intentos, el método de identificar gases por su coeficiente isoentrópico no es muy bueno porque es una variable poco discriminativa y la incertidumbre resultante es muy grande.

d) Determinar las capacidades térmicas molares del gas (a presión y a temperatura constantes).

>	W_:=subs(dat,subs(gamma=gamma__,dat,W__)):'W'=evalf(%,2);eqBE_:='n*c[v]*DT=W';n:=p1*V1/(R[u]*T1);n_:=subs(dat,p0*A*x1/(R[u]*T0)):'n'=evalf(%,2);cv_:=subs(dat,W_/(n_*DT));c[v,R12]=evalf(subs(g1dat,c[v]*M),3);c[v,R134a]=evalf(subs(g2dat,c[v]*M),3);c[p]='gamma*c[v]';cp_:=cv_*gamma__;

>

Como se vé, permanece la duda entre ambos gases.