>	restart:#"m1_np27"

Para mantener la presión de salida constante en una estación de suministro de gas suele usarse un gasómetro, que es un depósito invertido mantenido hidrostáticamente sobre una piscina que actúa de cierre hidrulico. Considérese a este fin un cilindro de hierro de 40 m de dimetro y 20 m de altura, cerrado por arriba y con una masa total de 500 toneladas, encerrando gas natural (aproxímese por metano puro), flotando boca abajo sobre una piscina de agua con 2 m de chapa hundidos (i.e. sobresalen 18 m de depsito). Se pide:
a) Estimar el espesor de la pared del depósito y la sobrepresión interior del gas.
b) Calcular el desnivel de líquido en el cierre hidráulico y la masa de gas encerrada.
c) Dar una expresión analítica sencilla que permita predecir la influencia de las variaciones de presión y temperatura atmosféricas sobre la altura aparente del gasmetro, a cantidad de gas fija, con aplicacin numrica para una variacin de 20 C y de 1 kPa.

d) Calcular la dilatación del depósito debida al efecto de las anteriores variaciones atmosféricas, sabiendo que el coeficiente de dilatación lineal del hierro es 12.10-6 K-1..

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="CH4":su2:="H2O":su3:="Hierro_fundido":dat:=[D=40*m_,L=20*m_,mD=500e3*kg_,zD1=18*m_,zM=660*m_,DTatm=20*K_,Dpatm=1e3*Pa_,alpha=12e-6/K_];

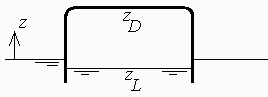
Esquema:

>

>

Eqs. const.:

>	eqET:=p*V=m*R*T;gdat:=get_gas_data(su1):ldat:=get_liq_data(su2):sdat:=get_sol_data(su3):dat:=op(dat),Const,gdat,SI2,SI1:'rho[S]'=subs(sdat,rho);

a) Estimar el espesor de la pared del depósito y la sobrepresión interior del gas.

>	eqmD:=mD=rho[S]*(Pi*D*L+Pi*D^2/4)*e;e_:=evalf(subs(rho[S]=rho,sdat,dat,solve(eqmD,e))):'e_'=evalf(%,2);eqBFs:=mD*g=Dp*Pi*D^2/4+rho[L]*g*(L-zD)*Pi*D*e;Dp_:=subs(dat,evalf(subs(e=e_,zD=zD1,rho[L]=rho,ldat,dat,solve(eqBFs,Dp))));

NB: el empuje hidrostático en el borde es despreciable.

b) Calcular el desnivel de líquido en el cierre hidráulico y la masa de gas encerrada.

>	eqBFw:=rho[L]*g*(-zL)=Dp;zL_:=subs(dat,evalf(subs(Dp=Dp_,zD=zD1,rho[L]=rho,ldat,dat,solve(eqBFw,zL)))):'zL_'=evalf(%,2);mG:=p*V/(R*T);mG:=(p0+Dp)*Pi*(D^2/4)*(zD-zL)/(R*T0);mG_:=evalf(subs(Dp=Dp_,zD=zD1,zL=zL_,dat,mG));

c) Dar una expresin analtica sencilla que permita predecir la influencia de las variaciones de presión y temperatura atmosféricas sobre la altura aparente del gasómetro, a cantidad de gas fija, con aplicacóin numérica para una variación de 20 C y de 1 kPa.

>	eqETG:=(patm+Dp)*V=m*R*Tatm;eqBFs:=dDp=0;eqBFw:=dzL=0;eqETG:=dpatm/p+dzD/zD=dTatm/T;dz_p:=-zD1/(p0+Dp);dz_Dp_:=subs(dat,subs(dpatm=Dpatm,dTatm=0,Dp=Dp_,dat,dz_p*Dpatm)):'dz_Dp_'=evalf(%,2);dz_T:=zD1/T0;dz_DT_:=subs(dat,subs(dTatm=DTatm,dpatm=0,dat,dz_T*DTatm)):'dz_T_'=evalf(%,2);

i.e. al subir la patm sube la pinterior (el Dp=4 kPa cte) y a T=cte ocupa menos luego baja.

Al subir la Tatm a p=cte se dilata el gas y sube.

d) Calcular la dilatación del depósito debida al efecto de las anteriores variaciones atmosféricas, sabiendo que el coeficiente de dilatación lineal del hierro es 12.10-6 K-1.

Tendrá lugar una dilatación uniforme del depósito; p.e. para el diámetro:

>	DD:=alpha*DTatm*D;DD_:=evalf(subs(dat,DD),2);

>