>	restart:interface(warnlevel=0):#"m1_np26"

Considérese un cilindro vertical, abierto por arriba, de 32,5 mm de dimetro y 10 cm de altura, en un ambiente a 20 C y 93 kPa, y un mbolo de grafito (r=2250 kg/m3) de 10 mm de espesor, inicialmente con su cara superior enrasada con el borde del cilindro, quedando una cierta cantidad de aire atrapado. Se pide:
a) Hacer un esquema del estado inicial. Calcular el coeficiente de dilatación del aire encerrado y el incremento de temperatura que dara lugar a la expulsión del mbolo.
b) En las condiciones iniciales, se deja caer una pesa de 300 g desde una altura de 5 cm sobre el mbolo. Razonar si en la evolucin se podra salir el mbolo del cilindro.
c) Deducir la relación pVg=cte, indicando de qu ecuaciones se parte y qué hipótesis se introducen.
d) Plantear las ecuaciones que permiten calcular la profundidad máxima alcanzable en el problema de la pesa.
e) Resolver el apartado anterior.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aire":dat:=[D=32.5e-3*m_,L=0.1*m_,T0=(20+273)*K_,p0=93e3*Pa_,rho[gra]=2250*kg_/m_^3,e=10e-3*m_,m[P]=0.3*kg_,H=5e-2*m_];

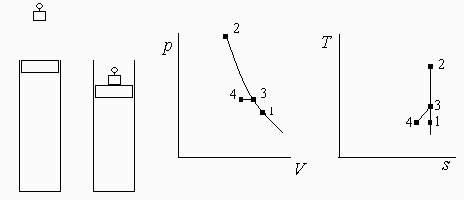
Esquema:

>

>

Eqs. const.:

>	eqET:=eq1_12;eqEE:=eq1_16;gdat:=get_gas_data(su1):dat:=op(dat),Const,gdat,SI2,SI1:

a) Hacer un esquema del estado inicial. Calcular el coeficiente de dilatacin del aire encerrado y el incremento de temperatura que dara lugar a la expulsin del mbolo.

>	V:=A*(L-e);A_:=evalf(subs(dat,Pi*D^2/4)):'A_'=evalf(%,2);V_:=subs(A=A_,dat,V):'V_'=evalf(%,2);alpha:=(1/'V')*Diff('V',T)[p];alpha[MGI]:=1/T;alpha_:=evalf(subs(T=T0,dat,1/T),2);DV:=A*e;DV_:=subs(dat,A_*e):'DV_'=evalf(%,2);eqDTlin:=DV=alpha*'V'*DT;DTlin_:=subs(dat,DV_/(alpha_*V_));

b) En las condiciones iniciales, se deja caer una pesa de 300 g desde una altura de 5 cm sobre el mbolo. Razonar si en la evolucin se podra salir el mbolo del cilindro.

Habría que comparar la energía cinética inicial del conjunto, que es menor que la de la pesa, con la necesaria para subir el conjunto émbolo+pesa la distancia del espesor; en principio, es posible que se salga.

c) Deducir la relacin pVg=cte, indicando de qu ecuaciones se parte y qu hiptesis se introducen.

>	V:='V':eqET:=p*V=m*R*T;'eqEE'=eqEE;eqBE:=DE=W+Q;eqA:=Q=0;eqWrev:=W=-Int(p,V);eqBE:=m*c[v]*dT=-p*dV;eqBE:=m*c[v]*dT=-(m*R*T/V)*dV;eqBE_:=dT/T=-(R/c[v])*dV/V;eq:=T*V^(R/c[v])=cte;eq:=T*V^(gamma-1)=cte;eq:=p*V^gamma=cte;

Se parte de eqET,eqEE y eqBE y se supone Q=0, Emdf=0 y sustancia calorficamente perfecta (c[p]=cte).

d) Plantear las ecuaciones que permiten calcular la profundidad mxima alcanzable en el problema de la pesa.

Sea z la posicin de la cara inferior del émbolo respecto al fondo del cilindro.

>

z1:=L-e;z1_:=subs(dat,z1);eqini:=p1=p0+m[E]*g/A;m[E]:=rho*A*e;m_[E]:=subs(dat,rho[gra]*A_*e):'m_[E]'=evalf(%,2);p1_:=subs(dat,p0+m_[E]*g/A_);m[EP]:='m[E]'+m[P];m_[EP]:=m_[E]+subs(dat,m[P]);eqBF:=-'m[P]'*sqrt(2*g*H)='m[EP]'*zp1;zp1_:=subs(dat,subs(dat,-m[P]*sqrt(2*g*H)/m_[EP])):'zp1_'=evalf(sqrt(subs(SI2,%^2)));eq1:=DE[EP]=W[EP]+Q[EP];eq1:=(1/2)*'m[EP]'*(0-'zp1'^2)+'m[EP]'*g*(z2-'z1')=Int(p*A,z='z1'..z2)-Int(p0*A,z='z1'..z2)-Int(Ff,z='z1'..z2);eq1:=(1/2)*'m[EP]'*(0-'zp1'^2)+'m[EP]'*g*(z2-'z1')=-(p2*z2*A-p1*'z1'*A)/(gamma-1)-p0*A*(z2-'z1');eq2:=p2*z2^gamma=p1*z1^gamma;

i.e. eq1 (BE del EP) y eq2 (evol-isentr-gas).

e) Resolver el apartado anterior.

>	eq12:=subs(p2=p1_*(z1/z2)^gamma,A=A_,dat,(1/2)*m_[EP]*(0-zp1_^2)+m_[EP]*g*(z2-z1_)=-(p2*z2*A-p1_*z1_*A)/(gamma-1)-p0*A*(z2-z1)):z2_:=fsolve(subs(SI0,eq12),z2=0..subs(SI0,z1_))*m_;

Aunque puede aproximarse a un movimiento armnico simple, se presenta a continuacin la integracin numrica completa con y sin friccin, hasta el equilibrio mecnico.

>	with(plots):

>

coe:=0:deq1:=diff(z(t),t)=zp(t):deq2:=m_[EP]*diff(zp(t),t)=-m_[EP]*g+(p-p0)*A_-coe*zp(t):ic1:=z(0)=z1_:ic2:=zp(0)=zp1_:eqs:=subs(dat,SI0,{deq1,subs(p=p1_*(z1_/z(t))^gamma,deq2),ic1,ic2}):dsol1:=dsolve(eqs,{z(t),zp(t)},numeric):odeplot(dsol1,[t,z(t)],0..0.1,numpoints=100,labels=["t(seg)","z(m)"],colour=black);

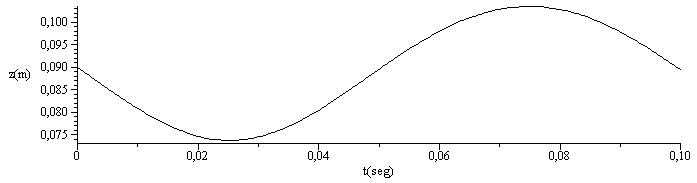como se aprecia en el gráfico, si la disipacin es pequea la parte inferior del émbolo saldría por encima del cilindro.

>

coe:=5:deq1:=diff(z(t),t)=zp(t):deq2:=m_[EP]*diff(zp(t),t)=-m_[EP]*g+(p-p0)*A_-coe*zp(t):ic1:=z(0)=z1_:ic2:=zp(0)=zp1_:eqs:=subs(dat,SI0,{deq1,subs(p=p1_*(z1_/z(t))^gamma,deq2),ic1,ic2}):dsol1:=dsolve(eqs,{z(t),zp(t)},numeric):odeplot(dsol1,[t,z(t)],0..0.5,numpoints=100,labels=["t(seg)","z(m)"],colour=black);

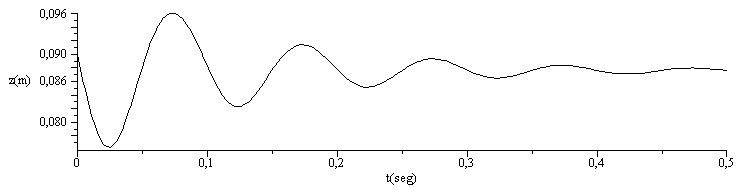Conclusin: en ausencia total de friccin llegaría a salirse, pero en cuanto roce bastante el émbolo no se saldría. Incluso si apenas rozase, posiblemente no se saldría porque al no rozar mucho tendría una fuga apreciable al comprimir y el planteamiento no sería adecuado.

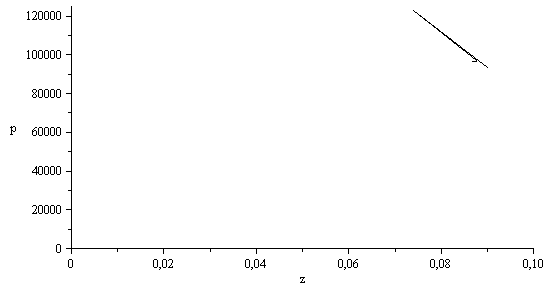
Puede apreciarse que las variaciones relativas de las magnitudes termodinámicas son pequeñas en un dibujo a escala:

>

p2_:=fsolve(subs(p1=p1_,z1=z1_,z2=z2_,dat,SI0,m_=1,eq2),p2=0..1e6)*Pa_;p3_:=subs(dat,p0+m_[EP]*g/A_);z3_:=fsolve(subs(p1=p1_,z1=z1_,p2=p3_,dat,SI0,m_=1,eq2),z2=0..0.1)*m_;p4_:='p3_';z4_:=z1_*p1_/p4_;plot(subs(SI0,m_=1,[[z1_,p1_],[z2_,p2_],[z3_,p3_],[z4_,p4_]]),'z'=0..0.1,'p'=0e3..125e3,color=black);

>

>