>	restart:#"m01_p20"

Se propone el experimento siguiente. A un matraz de 1000 cm3 se le conecta un tubo manométrico en forma de U, de 5 mm de diámetro interior y 1 m de longitud total, estando la parte más baja del tubo a 30 cm del otro extremo, y conteniendo 20 cm de columna de agua por cada lado de la U. Además, se ha instalado una resistencia eléctrica de 25 W y masa despreciable en el interior del matraz, conectada a una fuente de 5 V a través de un interruptor programable. Inicialmente todo está en equilibrio con el ambiente. Se pide:

a) Hacer un esquema de la instalación propuesta.

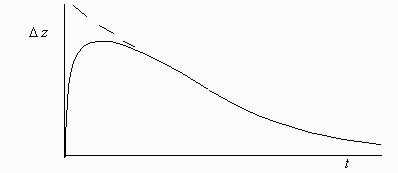
b) Describir la evolución del aire encerrado al suministrarle un impulso de corriente de 0,5 s de duración, dibujando además la evolución esperada de la posición del menisco.

c) Estimar los valores máximos de sobrepresión, expansión y temperatura media alcanzados

d) Suponiendo que las incertidumbres mayores son la de la medida manométrica (1 mm de columna de agua) y la del temporizador (0,05 s), estimar la incertidumbre asociada al cálculo de g (relación de capacidades térmicas) a partir de una medida manométrica de Dz=1 cm.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="Aire":su2:="H2O":dat:=[Vm=1000e-6*m_^3,Di=5e-3*m_,Ltot=1*m_,H=0.3*m_,z0=20e-2*m_,Res=25*Omega_,Volt=5*V_,Dt=0.5*s_,Dzexp=0.01*m_,DDz=0.001*m_,DDQ=0.05*J_]:dat:=[op(dat),A=evalf(subs(dat,Pi*Di^2/4))];

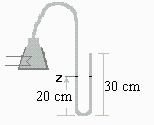
Esquema:

>

>

Ecs. const.:

>	eqET:=subs(eq1_11,eq1_12);eqEE:=eq1_16;gdat:=get_gas_data(su1):ldat:=get_liq_data(su2):dat:=op(dat),Const,gdat,ldat,SI2,SI1:

a) Hacer un esquema de la instalación propuesta.

b) Describir la evolución del aire encerrado al suministrarle un impulso de corriente de 0,5 s de duración, dibujando además la evolución esperada de la posición del menisco.

>	L0_:=subs(dat,(Ltot-H));Vae:=Vm+A*(L0-z0);V0_:=subs(L0=L0_,dat,Vae):'V0'=evalf(V0_,3);m:=subs(V0=V0_,gdat,dat,p0*V0/(R*T0)):'m'=evalf(m,2);Q_:=subs(dat,subs(dat,Omega_=V_^2/W_,Volt^2/Res*Dt)):'Q'=subs(SI0,evalf(Q_))*J_;

La resistencia eléctrica se calentará deprisa y se establecerá una convección natural que transmitirá pronto al aire la energía disipada, dilatándose éste contra el líquido manométrico.

c) Estimar los valores máximos de sobrepresión, expansión y temperatura media alcanzados.

>

W:=-Int(p(z),V=V1..V2);W:=-p0*DV;eqBE:=(p1*V1-p0*V0)/(gamma-1)=Q+W;eqBE:=(p*DV+V*Dp)/(gamma-1)=Q+W;DV:=A*Dz;Dp:=2*rho*g*Dz;Dz_:=solve(subs(p=p0,V=V0,T=T0,eqBE),Dz);Dz__:=subs(Q=Q_,V0=V0_,dat,Dz_):'Dz'=evalf(Dz__,2);DV_:=subs(dat,Dz__*A):'DV'=evalf(DV_,2);Dp_:=subs(dat,rho*g*Dz__):'Dp'=evalf(Dp_,3);W_:=subs(dat,-p0*A*Dz__):'W'=evalf(W_,2);DT_:=subs(dat,(W_+Q_)/(m*c[v]));

d) Suponiendo que las incertidumbres mayores son la de la medida manométrica (1 mm de columna de agua) y la del temporizador (0,05 s), estimar la incertidumbre asociada al cálculo de g (relación de capacidades térmicas) a partir de una medida manométrica de Dz=1 cm.

>

gamma_:=solve(subs(gamma=gam,p0=p,eqBE),gam):'gamma'=%;gamma__:=subs(p=p0,V=Vm,Dz=Dzexp,gamma_);gamma___:=subs(Q=Q_,dat,gamma__):'gamma'=evalf(gamma___,3);sigma[gamma]:=sqrt((Diff(gamma,Dz)*sigma[Dz])^2+(Diff(gamma,Q)*sigma[Q])^2);Dg_DDz:=subs(Q=Q_,dat,diff(gamma__,Dzexp)):Diff(gamma,Dz)[Q]=evalf(%,2);Dg_DQ:=subs(Q=Q_,dat,diff(gamma__,Q)):Diff(gamma,Q)[Dz]=evalf(%,2);subs(dat,sqrt((Dg_DDz*DDz)^2+(Dg_DQ*DDQ)^2)):'sigma[gamma]'=evalf(%);

>

es decir, gamma=[1,38..1,52]; presumiblemente aire (gamma=1,40).