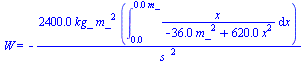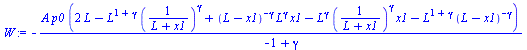>	restart:interface(warnlevel=0):#"m01_p16"

Se tiene un cilindro horizontal de 1 cm de diámetro y 50 cm de largo, cerrado por ambos extremos, dentro del cual, un émbolo de acero imantado de 2 cm de espesor separa dos masas iguales de aire, inicialmente a To=Tamb y po=pamb., y se pretende desplazar el émbolo 1 cm hacia un lado, con ayuda de un dispositivo electromagnético, y después (ya atemperado el sistema) soltarlo. Se pide:

a) Determinar la fuerza necesaria y el trabajo requerido para mover el émbolo en el caso de realizar el proceso lentamente.

b) Determinar la fuerza necesaria y el trabajo requerido para mover el émbolo en el caso de realizar el proceso rápidamente.

c) Velocidad y aceleración del émbolo en la posición de suelta y en el instante del primer paso por el punto medio del cilindro.

e) Integrar las ecuaciones del movimiento del émbolo y representar la posición en función del tiempo, suponiéndo que la fuerza de fricción es proporcional a la velocidad del émbolo, con un coeficiente de 10 N/(m/s).

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma):

>	su1:="Aire":su2:="Acero_inox":dat:=[Di=0.01*m_,Ltotal=0.5*m_,Le=0.02*m_,x1=0.01*m_,coef=0.1*N_/(m_/s_)]:dat:=[op(dat),L=subs(dat,(Ltotal-Le)/2),A=evalf(subs(dat,Pi*Di^2/4))];

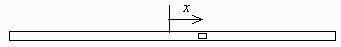
Esquema:

>

>

Ecs. const.:

>	eqET:=subs(eq1_11,eq1_12);eqEE:=eq1_16;gdat:=get_gas_data(su1):sdat:=get_sol_data(su2):mE_:=subs(dat,sdat,A*Le*rho);dat:=op(dat),mE=mE_,Const,gdat,SI2,SI1:

a) Determinar la fuerza necesaria y el trabajo requerido para mover el émbolo en el caso de realizar el proceso lentamente.

>	p1(x):=p0*L/(L+x);p1lin(x):=collect(convert(series(p1(x),x=0,2),polynom),p0);

>	p2(x):=p0*L/(L-x);p2lin(x):=collect(convert(series(p2(x),x=0,2),polynom),p0);

>

p11_:=evalf(subs(x=x1,dat,p1(x))):p21_:=evalf(subs(x=x1,dat,p2(x))):p11lin_:=evalf(subs(x=x1,dat,p1lin(x))):p21lin_:=evalf(subs(x=x1,dat,p2lin(x))):'p11'=evalf(p11_/(1e3*Pa_/kPa_),3);'p21'=evalf(p21_/(1e3*Pa_/kPa_),4);'p11lin'=evalf(p11lin_/(1e3*Pa_/kPa_),3);'p12lin'=evalf(p21lin_/(1e3*Pa_/kPa_),4);

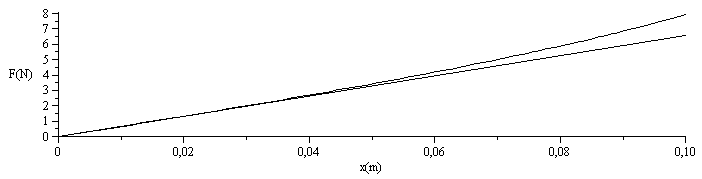
La fuerza necesaria, suponiendo despreciable el rozamiento del émbolo con la pared,  será:

>	Fnon(x):='(p2(x)-p1(x))*A';Fnon(x):=collect(eval(Fnon(x)),p0);Fnon_(x):=subs(dat,SI0,Fnon(x)):Flin(x):=expand((p2lin(x)-p1lin(x))*A);Flin_(x):=subs(dat,SI0,Flin(x)):plot([Fnon_(x),Flin_(x)],x=0..0.1,labels=["x(m)","F(N)"],colour=black);

cuyo valor máximo es F(x1)=0,66 N (F(x1)=0,65 N con el modelo lineal).

>	F_:=subs(SI1,evalf(subs(x=x1,dat,Fnon(x))));Flin_:=subs(SI1,evalf(subs(x=x1,dat,Flin(x))));

El trabajo consumido (despreciando el rozamiento) será:

>	assume(x1<L,L>0):W:=Int('Fnon(x)',x=0..x1);W:=(combine(factor(value(W)),ln));Wlin:=int(Flin(x),x=0..x1);

resultando un valor de W=3,3.10-3 J en ambos modelos.

>	W_:=subs(SI1,evalf(simplify(subs(dat,W)))):'W'=evalf(W_,2);Wlin_:=subs(SI1,evalf(subs(dat,Wlin)));

b) Determinar la fuerza necesaria y el trabajo requerido para mover el émbolo en el caso de realizar el proceso rápidamente.

>	p1(x):=p0*(L/(L+x))^gamma;p1lin(x):=collect(convert(series(p1(x),x=0,2),polynom),p0);

>	p2(x):=p0*(L/(L-x))^gamma;p2lin(x):=collect(convert(series(p2(x),x=0,2),polynom),p0);

>

p11_:=evalf(subs(x=x1,dat,p1(x))):p21_:=evalf(subs(x=x1,dat,p2(x))):p11lin_:=evalf(subs(x=x1,dat,p1lin(x))):p21lin_:=evalf(subs(x=x1,dat,p2lin(x))):'p11'=evalf(p11_/(1000*Pa_/kPa_),3);'p21'=evalf(p21_/(1000*Pa_/kPa_),4);'p11lin'=evalf(p11lin_/(1000*Pa_/kPa_),3);'p21lin'=evalf(p21lin_/(1000*Pa_/kPa_),4);

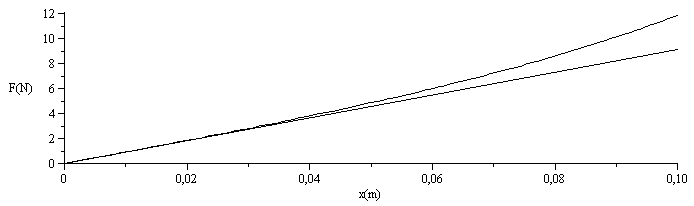
La fuerza necesaria (despreciando el rozamiento) será:

>	Fnon(x):='(p2(x)-p1(x))*A';Fnon(x):=collect(eval(Fnon(x)),p0);Fnon_(x):=subs(dat,SI0,Fnon(x)):Flin(x):=expand((p2lin(x)-p1lin(x))*A);Flin__(x):=subs(dat,SI0,Flin(x)):plot([Fnon_(x),Flin__(x)],x=0..0.1,labels=["x(m)","F(N)"],colour=black);

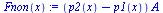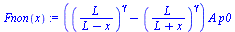cuyo valor máximo es F(x1)=0,92 N en ambos modelos.

>	F_:=subs(SI1,evalf(subs(x=x1,dat,Fnon(x))));Flin_:=subs(SI1,evalf(subs(x=x1,dat,Flin(x))));

El trabajo consumido (despreciando el rozamiento) será:

>	W:=Int('Fnon(x)',x=0..x1);eval(W);W:=simplify(expand(value(W)));Wlin:=int(Flin(x),x=0..x1);W_:=evalf(subs(x=x1,dat,SI0,W))*J_:Wlin_:=subs(SI1,evalf(subs(x=x1,dat,Wlin))):'W'=evalf(W_,2);

c) Velocidad y aceleración del émbolo en la posición de suelta y en el instante del primer paso por el punto medio del cilindro.

>	p10:=p0*(L/(L+x1));p1(x):=p10*((L+x1)/(L+x))^gamma;p1lin_1(x):=factor(convert(series(p1(x),x=0,2),polynom));p1lin_2(x):=expand(convert(series(p1lin_1(x),x1=0,2),polynom));p1lin(x):=collect(subsop(4=0,6=0,p1lin_2(x)),{p0});

>	p20:=p0*(L/(L-x1));p2(x):=p20*((L-x1)/(L-x))^gamma;p2lin_1(x):=factor(convert(series(p2(x),x=0,2),polynom));p2lin_2(x):=expand(convert(series(p2lin_1(x),x1=0,2),polynom));p2lin(x):=collect(subsop(4=0,6=0,p2lin_2(x)),{p0});

>

eqM:=mE*diff(x(t),t,t)=Fu(x);xp2-xp20=Int(2*diff(x(t),t,t),x=x1..0);eqE:=Ec-Ec0=Int(Fu(x),x=x1..x);acellin(x):=factor(expand((p1lin(x)-p2lin(x))*A/mE));acellinx1:=convert(series(subs(x=x1,acellin(x)),x1,2),polynom);acellin0:=convert(series(subs(x=0,acellin(x)),x1,2),polynom);vellin0:=convert(series(sqrt(2*int(acellin(x),x=x1..0)),x1,2),polynom);

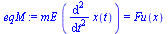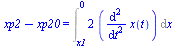>	gamma_:=subs(dat,gamma):deqlin:=mE*diff(x(t),t,t)='(p1lin(x)-p2lin(x))*A';deqlin:=mE*diff(x(t),t,t)=factor(subs(x=x(t),(p1lin(x)-p2lin(x))*A));gamma:=omega^2/2/A/p0*mE*L:expand(deqlin/mE);

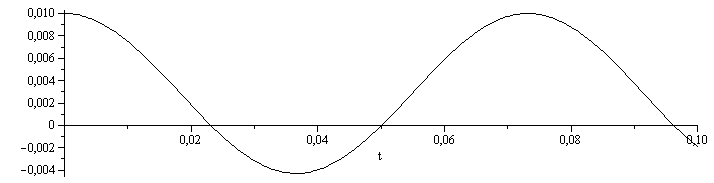
>	sol1:=dsolve({expand(deqlin)/mE,x(0)=x1,D(x)(0)=0},x(t));omega:=sqrt(2*ga_*A*p0/mE/L);xlin(t):=rhs(sol1);T:=2*Pi/omega;T_:=evalf(subs(ga_=gamma_,dat,SI0,T))*s_;plot(subs(ga_=gamma_,dat,SI0,xlin(t)),t=0..0.1,color=black);

>

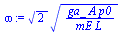acellin0_:=subs(ga_=gamma_,dat,acellin0):'acellin0'=evalf(acellin0_,4);acellinx1_:=subs(ga_=gamma_,dat,acellinx1):'acellinx1'=evalf(acellinx1_,4);vellin0_:=evalf(subs(ga_=gamma_,dat,SI0,vellin0))*m_/s_:'vellin0'=evalf(vellin0_,2);x_acellin_0:=solve(subs(dat,acellin(x))=0,x):'x_acellin_0'=evalf(x_acellin_0,2);

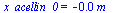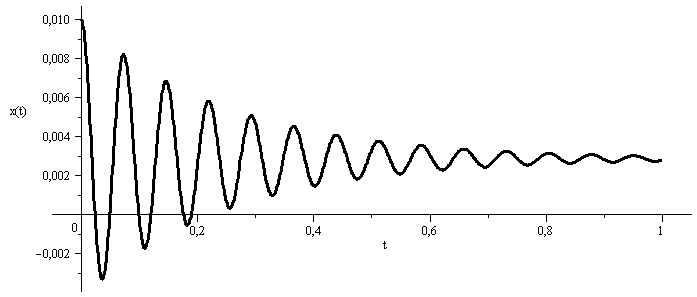
e) Integrar las ecuaciones del movimiento del émbolo y representar la posición en función del tiempo, suponiéndo que la fuerza de fricción es proporcional a la velocidad del émbolo, con un coeficiente de 10 N/(m/s).

>	gamma:='gamma':deq1:=mE*diff(x(t),t,t)='(p1(x)-p2(x))*A-coef*diff(x(t),t)';deq1_:=subs(dat,SI0,deq1);

>	with(DEtools):DEplot(deq1_,x(t),t=0..1,{[x(0)=subs(dat,x1)/m_,D(x)(0)=0]},stepsize=0.001,linecolour=black);

>	x_acel0_:=fsolve(subs(dat,SI0,(p1(x)-p2(x))*A),x=0..0.03)*m_:'x_acel0'=evalf(x_acel0_);

>

Int1:='int(p1(x)*A,x=x1..x_acel0_)';Int1_:=subs(dat,SI0,Int1)*J_:'Int1'=evalf(Int1_,2);Int2:='int(p2(x)*A,x=x1..x_acel0_)';Int2_:=subs(dat,SI0,Int2)*J_:'Int2'=evalf(Int2_,2);DInt12_:=Int1_-Int2_;Ec_xacel0_:=subs(dat,mE*subs(dat,sqrt(2*int(acellin(x),x=x1..x_acel0_)))^2/2);Emdf_xacel0_:=DInt12_-Ec_xacel0_;

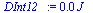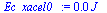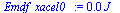Baja fricción quiere decir Emdf<<Ecmax.

Se puede estimar el tiempo de relajación por coef*vel^2*t=Ec.

>	t_:=subs(dat,Ec_xacel0_/(coef*vellin0_^2));

>