>	restart:#"m01_p09"

Se dispone de un cilindro horizontal de 15 cm2 de sección y 40 cm de largo, cerrado por un extremo. En el otro extremo se coloca un émbolo de hierro de 1 cm de espesor y se empuja hasta conseguir llevarlo a 5 cm del fondo, comprimiendo el aire encerrado. Se pide:

a) Trabajo que sería necesario aportar (neto, p.e., desde un depósito mecánico reversible) suponiendo que la compresión fuese muy rápida.

b) Como en a), pero suponiendo que la compresión fuese muy lenta.

c) Exergía de la configuración final (atemperada)

d) Supóngase que desde este último estado se suelta el émbolo; calcular la aceleración inicial y la posición en la que se alcanzaría la velocidad máxima.

e) Velocidad máxima y velocidad a la salida.

f) Representar la posición y la velocidad en función del tiempo

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aire":su2:="Hierro_fundido":dat:=[A=0.0015*m_^2,L=0.4*m_,e=0.01*m_,x1=0.05*m_]:dat:=[op(dat),x0=subs(dat,L-e*0),mE=subs(dat,rho*A*e)];

Esquema:

>

>

Eqs. const.:

>	eqET:=subs(eq1_11,eq1_12);eqEE:=eq1_16;gdat:=get_gas_data(su1):sdat:=get_sol_data(su2):dat:=op(dat),Const,gdat,sdat,SI2,SI1:rho_:=subs(dat,rho);dat:=op(subs('rho'=rho_,[dat])):mE_:=subs(dat,mE);

a) Trabajo que sería necesario aportar (neto, p.e., desde un depósito mecánico reversible) suponiendo que la compresión fuese muy rápida.

>	T1:=T0*(x0/x1)^(gamma-1);T1_:=evalf(subs(dat,T1));p1:=p0*(x0/x1)^gamma;p1_:=evalf(subs(dat,p1)):p1__:=evalf(%/(1e3*Pa_/kPa_));

>	W1:=Int((p0*(x0/x)^gamma-p0)*A,x=x0..x1);W1:=int((p0*(x0/x)^gamma-p0)*A,x=x0..x1);W1_:=subs(dat,evalf(subs(dat,W1)));

b) Como en a), pero suponiendo que la compresión fuese muy lenta.

>	T1:=T0;T1_:=evalf(subs(dat,T1));p1:=p0*(x0/x1);p1_:=evalf(subs(dat,p1)):p1__:=evalf(%/(1e3*Pa_/kPa_));dat:=op([dat]),'p1'=p1_:

>	W1:=Int((p0*(x0/x)-p0)*A,x=x0..x1);W1:=int((p0*(x0/x)-p0)*A,x=x0..x1);W1_:=evalf(subs(dat,SI0,W1))*J_;

c) Exergía de la configuración final (atemperada).

NOTA. Esta pregunta no es del tema 1 (Energía). (Puede pasar al siguiente apartado).

>	DPhi:=W1_;DPhi:=DE+p0*DV-T0*DS;DPhi_:=subs(DE=0,DV=A*x1*(1-p1/p0),DS=-m*R*ln(p1/p0),DPhi);DPhi__:=subs(SI2,SI1,evalf(subs(m=p0*A*x0/R/T0,dat,%)));

d) Supóngase que desde este último estado se suelta el émbolo; calcular la aceleración inicial y la posición en la que se alcanzaría la velocidad máxima.

>	acel:=A*(p-p0)/mE;acel:=A*(p1*(x1/x)^gamma-p0)/mE;acel0_:=subs(dat,evalf(subs(x=x1,dat,acel)));

>	x_velmax:=solve(acel=0,x);x_velmax_:=evalf(subs(dat,x_velmax));

e) Velocidad máxima y velocidad a la salida.

>	deq1:=diff(x(t),t)=xp(t);deq2:=diff(xp(t),t)=subs(x=x(t),acel);deq1_:=deq1:deq2_:=subs(dat,SI0,deq2);ic1:=x(0)=x1;ic2:=xp(0)=0;ic1_:=subs(dat,SI0,ic1);ic2_:=ic2:

>	dsol1:=dsolve({deq1_,deq2_,ic1_,ic2_},{x(t),xp(t)},numeric);

(se ha hecho como si no escapara.)

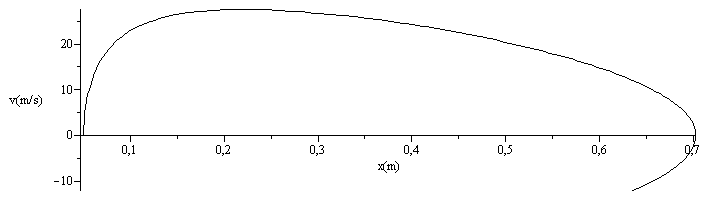
>	with(plots):odeplot(dsol1,[t,x(t)],0..0.1,numpoints=100,labels=["t(s)","x(m)"],colour=black);odeplot(dsol1,[t,xp(t)],0..0.1,numpoints=100,labels=["t(s)","v(m/s)"],colour=black);odeplot(dsol1,[x(t),xp(t)],0..0.05,numpoints=100,labels=["x(m)","v(m/s)"],colour=black);

Warning, the name changecoords has been redefined

>	Ec:=Int(mE*acel,x=x1..x);Ec:=int(mE*acel,x=x1..x2);vel:=sqrt('2*Ec/mE');

>	vel_:=evalf(subs(dat,SI0,vel));velmax_:=evalf(subs(x2=x_velmax_/m_,vel_))*m_/s_;velsal_:=evalf(subs(x2=subs(dat,x0)/m_,vel_))*m_/s_;

f) Representar la posición y la velocidad en función del tiempo

>	plot([vel_,[[x_velmax_/m_,0],[x_velmax_/m_,30]],[[subs(dat,x0)/m_,0],[subs(dat,x0)/m_,30]]],x2=0..0.7,labels=["t(s)","v(m/s)"],colour=black);

>