>	restart:#"m01_p07"

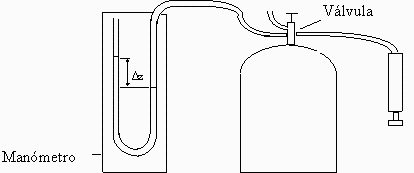
Dentro de un recipiente de 10 litros hay un gas desconocido que está inicialmente a una sobrepresión de 50 kPa respecto a la atmósfera, que está a 15 ºC y 100 kPa. En una maniobra rápida, se deja escapar algo de gas hasta que la presión manométrica es de 40 kPa, cerrándose la válvula entonces y observándose que la presión manométrica se estabiliza en 44 kPa. Se pide:
a) Deducir qué tipo de gas hay dentro a partir de la relación de capacidades térmicas a presión y a volumen constante del gas.
b) Temperatura interior en el momento de cerrar la válvula.
c) Masa de gas perdido.
d) Calor intercambiado por el gas durante todo el proceso.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	datP:=[V=0.01*m_^3,Dp1=50e3*Pa_,Dp2=40e3*Pa_,Dp3=0.44e5*Pa_]:datG:=[V=0.01*m_^3,Dp1=50e3*Pa_,Dp2=40e3*Pa_,ga=5/3]:

a) Deducir qué tipo de gas hay dentro a partir de la relación de capacidades térmicas a presión y a volumen constante del gas.
Hay que llevar cuidado porque es muy sensible a los errores de redondeo.

Deducir ga conocido Dp3: #Doesn't work with gamma!!

>

eq1:=T2/T1=(p2/p1)^((ga-1)/ga);eq2:=T3/T2=p3/p2;p1:=p0+Dp1;p1_:=subs(Const,datP,p1);T1:=T0;T1_:=subs(Const,datP,T1);p2:=p0+Dp2;p2_:=subs(Const,datP,p2);p3:=p0+Dp3;p3_:=subs(Const,datP,p3);sol1:=solve({eq1,eq2},{T2,T3});ga_:=solve(subs(sol1,Const,datP,T3=T1),ga):'gamma'=evalf(%,3);sol1__:=subs(Const,datP,ga=ga_,sol1);assign(%):

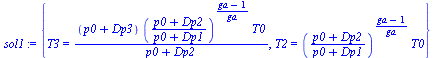Como ga=5/3 es un gas monoatómico que presumiblemente será argón (por el precio, luego:

c) Masa de gas perdido.

>	datg:=get_gas_data("Ar"):m1_:=evalf(subs(datg,datP,datG,SI2,p1_*V/(R*T1_))):m1__:=evalf(%*1000*g_/kg_,2);m2_:=evalf(subs(datg,datP,datG,SI2,p2_*V/(R*T2))):m2__:=evalf(%*1000*g_/kg_,2);Dm_:=m2_-m1_:Dm__:=evalf(%*1000*g_/kg_,2);

d) Calor intercambiado por el gas durante todo el proceso.

>	Q12:=0;eqBE:=DE=Q+W;Q23:='m2*c[v]*(T0-T2)';Q23_:=evalf(subs(datg,m2_*c[v]*(T1_-T2)));

Efecto del redondeo: supongamos conocido gamma y calculemos Dp3.

>

p1:=p0+Dp1;p1_:=subs(Const,datG,p1);T1:=T0;T1_:=subs(Const,datG,T1);p2:=p0+Dp2;p2_:=subs(Const,datG,p2);T2:=T1*(p2/p1)^((ga-1)/ga);T2_:=subs(Const,datP,T2):p3:=p0+Dp3;p3_:=subs(Const,datG,p3);T3:=T2*(p3/p2);Dp3:=solve(T3=T1,Dp3);Dp3_:=evalf(subs(Const,datG,Dp3)):Dp3__:=evalf(%/(1000*Pa_/kPa_));T3_:=subs(Const,datG,T3):T2_:=evalf(subs(Const,datG,T2));

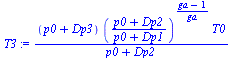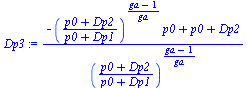c) Masa de gas perdido.

Suponiendo que fuera argón.

>	datg:=get_gas_data("Ar"):m1_:=evalf(subs(datg,datP,datG,SI2,p1_*V/(R*T1_))):m1__:=evalf(%*1000*g_/kg_);m2_:=evalf(subs(datg,datP,datG,SI2,p2_*V/(R*T2_))):m2__:=evalf(%*1000*g_/kg_);Dm_:=m2_-m1_:Dm__:=evalf(%*1000*g_/kg_);

d) Calor intercambiado por el gas durante todo el proceso.

>	Q12:=0;eqBE:=DE=Q+W;Q23:='m2*c[v]*(T0-T2)';Q23_:=evalf(subs(datg,m2_*c[v]*(T1_-T2_)));

NOTA ADDICIONAL

Este procedimiento experimental de determinación de cp/cv se llama de Clément-Desormes, y se hace en muchas clases prácticas de Termodinámica. Históricamente, sin embargo, el experimento original de Charles-Bernard Desormes y Nicolas Clement, hacia 1794, se basaba en la compresión rápida del gas en el recipiente previamente evacuado, en lugar de en la expansión rápida del gas comprimido (si se hubiese hecho el vacío, en la compresión desde la atmósfera se alcanzararía Tmax=gamma*Tatm).

>