>	restart:#"m01_p06"

En un colector solar de 20 m2, una corriente de aire recibe calor a razón de  , siendo  =500 W.m 2 y t la hora del día (se supone que desde las 6 de la tarde a las 6 de la mañana se desconecta el colector). El aire cede calor a un acumulador térmico de 2 m3 de agua, con el que se trata de suministrar calor desde las 6 de la tarde a las 6 de la mañana a un local que está a 20 ºC en un ambiente a 10 ºC. Suponiendo que la temperatura mínima del acumulador es de 30 ºC, se pide:

a)  Intensidad de la carga térmica admisible y temperatura del acumulador en función del tiempo, suponiendo que el consumo de energía térmica es constante en el periodo indicado. Representación gráfica.

b) Variación de la temperatura del acumulador con el tiempo, suponiendo que el consumo de energía térmica en el periodo indicado es proporcional a la diferencia entre la temperatura del acumulador y la del local, calculando el factor de proporcionalidad. Representación gráfica.

c)•Indicar cómo se calcularía la variación de la temperatura del acumulador con el tiempo, suponiendo que el consumo de energía térmica en el periodo indicado es proporcional a la diferencia entre la temperatura del acumulador y la del local, y teniendo en cuenta unas pérdidas del acumulador proporcionales a la diferencia entre su temperatura y la del ambiente (conocida la constante de proporcionalidad).

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):assume(t>0,t6>0,t18=3*t6,t24=4*t6);

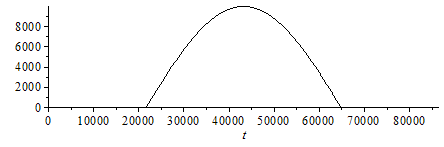
>	su:="H2O":dat:=[A=20*m_^2,q0=500*W_/m_^2,m=2000*kg_,T20=(20+273)*K_,T30=(30+273)*K_,T10=(10+273)*K_,t6=6*3600*s_,t18=18*3600*s_,t24=24*3600*s_]:dat:=[op(dat),Q0=subs(dat,q0*A)];Qin:=piecewise(t<t6,0,t>t18,0,Q0*sin(2*Pi*(t-t6)/t24));plot(subs(dat,SI0,Qin),t=0..24*3600,color=black);

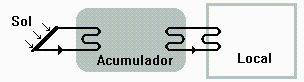
Esquema:

>

Eqs. const.:

>	eqET:=eq1_15;eqBE:=eq1_17;ldat:=get_liq_data(su):dat:=op(dat),mc=subs(dat,ldat,m*c),Const,ldat,SI2,SI1:

a) •Intensidad de la carga térmica admisible y temperatura del acumulador en función del tiempo, suponiendo que el consumo de energía térmica es constante en el periodo indicado. Representación gráfica.

Si, en lugar de lo dicho en este enunciado, fuese Qout=cte durante las 24 h.

Hipót.: Periódico de 24 h.

>

Qin_int:=int(Qin,t=0..t24);Qin_int_:=subs(dat,SI1,evalf(subs(dat,Qin_int)))/(1e6*J_/MJ_);Qout1:=Qin_int/t24;Qout1_:=subs(dat,evalf(subs(dat,%)));eqBEacum:=m*c*dT/dt='Qin-Qout';deq1:=diff(T1(t),t)=(Qin-Qout1)/(mc);dsol1:=simplify(dsolve({deq1,T1(0)=T[t0]},T1(t)));assign(%):eqminmax:='Qin=Qout';tmin:=fsolve(subs(dat,SI0,Qin=Qout1),t=0..12*3600)*s_:'tmin'=evalf(%);tmin_h:=evalf(tmin/(3600*s_/h_));tmax:=evalf(subs(dat,t24-tmin));tmax_h:=evalf(tmax/(3600*s_/h_));Tmin:=evalf(expand(subs(dat,SI0,subs(t=tmin,dat,T1(t)))));Tmax:=evalf(expand(subs(t=tmax,dat,SI0,T1(t))));Tmax_Tmin:=(Tmax-Tmin)*K_;

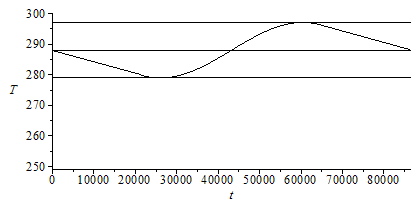
Suponiendo que la temperatura a medianoche (t=0) fuese de T[t0]=288 K (15 ºC).

>	plot(subs(T[t0]=T0,dat,SI0,{T1(t),[[0,Tmin],[t24,Tmin]],[[0,Tmax],[t24,Tmax]],[[0,T0],[t24,T0]]}),t=0..86400,T=250..300,colour=black);

Ahora con Qout=cte desde las 18 h a las 6 h.

>

Qout2:=piecewise(t<t6,Qout20,t>t18,Qout20,0);plot(subs(Qout20=1,dat,SI0,Qout2),t=0..24*3600,color=black);Qout_int:=int(subs(t18=3/4*t24,t6=1/4*t24,Qout2),t=0..t24);Qout20_:=solve(Qin_int=Qout_int,Qout20);Qout20__:=subs(dat,evalf(subs(dat,Qout20_)));deq1:=diff(T2(t),t)=(Qin-Qout2)/(mc);dsol1:=simplify(dsolve({subs(t18=3*t6,t24=4*t6,deq1),T2(t6)=T6},T2(t)));

>

Tmin:=T30=T6;eqmin:=subs(dat,T6=T30);tmin:=t6;Tmax:=round(evalf(subs(dat,simplify(subs(dsol1,Qout20=Qout20__,t=t24-tmin,eqmin,dat,SI0,T2(t))))))*K_;Tmax_Tmin:=subs(eqmin,Tmax-rhs(Tmin));Tmean:=round(subs(eqmin,(Tmax+rhs(Tmin))/2/K_))*K_;'Tmean'=TKC(%);T2_(t):=subs(dsol1,Qout20=Qout20__,dat,eqmin,dat,SI0,T2(t)):plot(subs(dat,SI0,{[[0,T30],[t24,T30]],[[0,Tmean],[t24,Tmean]],[[0,Tmax],[t24,Tmax]],T2_(t)}),t=0..86400,'T'=300..350,color=black);

b) Variación de la temperatura del acumulador con el tiempo, suponiendo que el consumo de energía térmica en el periodo indicado es proporcional a la diferencia entre la temperatura del acumulador y la del local, calculando el factor de proporcionalidad. Representación gráfica

Qout=K*(T-T20)  from 18 h to 6 h.

>	Qout3:=piecewise(t<t6 or t>t18,K*(T(t)-T20),0);#Doesn't wotk all at once

>

Qin:=Q0*sin(2*Pi*(t-t6)/t24);Qout:=K*(T(t)-T20);deq3:=diff(T3(t),t)=(0-K*(T3(t)-T20))/(mc);dsol3:=simplify(dsolve({subs(t18=3*t6,t24=4*t6,deq3),T3(t6)=T6},T3(t)));deq4:=diff(T4(t),t)=(Qin-0)/(mc);dsol4:=simplify(dsolve({subs(t18=3*t6,t24=4*t6,deq4),T4(t6)=T6},T4(t)));T18:=evalf(subs(dsol4,eqmin,t=t18,dat,SI2,T4(t))):T18_=evalf(%);deq5:=diff(T5(t),t)=(0-K*(T5(t)-T20))/(mc);dsol5:=simplify(dsolve({subs(t18=3*t6,t24=4*t6,deq5),T5(t18)=T18_},T5(t)));subs(dsol5,t=t24,T5(t));K0:=fsolve(subs(SI0,evalf(subs(dsol5,T18_=T18,t=t24,T6=T30,dat,SI2,T5(t))=subs(dsol3,t=0,T6=T30,dat,SI2,T3(t)))),K)*W_/K_:K0_:=evalf(%,2);

>

T3_(t):=subs(evalf(subs(dsol3,T6=T30,K=K0,dat,SI2,T3(t))));T3_0:=evalf(subs(t=0,T3_(t))):'T3_0'=evalf(%,3);T4_(t):=simplify(subs(evalf(subs(dsol4,T6=T30,K=K0,dat,SI2,T4(t)))));T5_(t):=subs(evalf(subs(dsol5,T18_=T18,T6=T30,K=K0,dat,SI2,T5(t))));plot(subs(dat,SI0,{[[0,T30],[t24,T30]],[[0,Tmean],[t24,Tmean]],[[0,Tmax],[t24,Tmax]],T3_(t),T4_(t),T5_(t)}),t=-6*3600..86400,'T'=300..350,colour=black);

Qout=K*(T-T20)  from 18 h to 6 h plus k*(T-T0) during the 24 h can be done similarly.

>