>	restart:#"m01_p05".

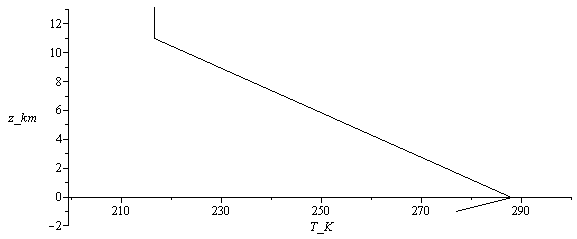
Considérese el mar y la atmósfera terrestre, y admítase que la variación de la temperatura con la altura es lineal y tal que a 1 km de profundidad vale 4 °C, a nivel del mar vale 15 °C, a 11 km de altura vale  56,5 °C y a partir de 20 km de altura vuelve a aumentar. Se pide:

a) Recuérdese la ecuación del equilibrio hidrostático para determinar la variación de la presión con la altura. ¿Influye la variación de la gravedad con la altura?

b) El estado descrito ¿es de equilibrio, o meramente estacionario? ¿Cómo se interpreta que el perfil de temperatura tenga un máximo local a nivel del mar, a la luz de la transmisión de calor y el balance energético?

c) ¿Qué espesor de hidrosfera tiene la misma capacidad térmica que toda la atmósfera?

d) Si el barómetro de un avión marca media atmósfera, ¿a qué altura vuela?

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):

>	su1:="Aire":su2:="H2O":dat:=[z_1=-1000*m_,T_1=(4+273)*K_,z11=11000*m_,T11=(-56.5+273)*K_,z20=20000*m_]:dat:=[op(dat),T20=subs(dat,T11)];

Esquema:

>	plot(subs(dat,Const,[[[T_1/K_,-1],[T0/K_,0]],[[T0/K_,0],[T11/K_,11]],[[T11/K_,11],[T20/K_,20]]]),'T_K'=200..300,z_km=-2..13,color=black);

>

>

Eqs. const.:

>	eqETaire:=eq1_12;eqEEaire:=eq1_16;eqETagua:=eq1_15;eqEEagua:=eq1_17;gdat:=get_gas_data(su1):ldat:=op(subs(eqETagua,[get_liq_data(su2)])):dat:=op(dat),Const,gdat,ldat,SI2,SI1:

a) Recuérdese la ecuación del equilibrio hidrostático para determinar la variación de la presión con la altura. ¿Influye la variación de la gravedad con la altura?

En el agua:

>	eqBF:=diff(p(z),z)=-rho*g;sol1:=dsolve({subs(eqETagua,eqBF),p(0)=p0},p(z));

En la atmósfera:

>	sol2:=(dsolve({subs(p=p(z),T=T0+(T11-T0)*(z/z11),subs(eqETaire,subs(p(z)=p,eqBF))),p(0)=p0},p(z)));

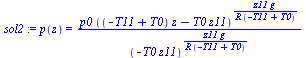En la estratosfera:

>	sol3:=dsolve({subs(p=p(z),T=T11,subs(eqETaire,subs(p(z)=p,eqBF))),p(z11)=p11},p(z));

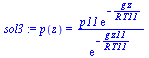Valores numéricos:

En el mar:

>	sol1_:=evalf(subs(dat,SI0,sol1));sol1_1:=subs(z=z_1,dat,lhs(%))=evalf(subs(z=z_1,dat,SI0,rhs(%))/1000*kPa_);

>

i.e. unos 10 MPa a 100 m de profundidad.

En la atmósfera:

>	sol2_:=subs(dat,sol2);sol2_11:=p(z11)=p0*(T11/T0)^(z11*g/(R*(T0-T11)));for i from 0 to 11 by 1 do cat(p,i)=Re(subs(z=i*1000,SI0,rhs(sol2_)))*Pa_;od;

o, en forma más resumida (y revertida):

>	eqp:=p/p0=(1-(1-T11/T0)*(z/z11))^((g*z11)/(R*(T0-T11)));p5km:=solve(subs(z=1300,dat,SI0,%))*Pa_;%*0.21;eqz:=z/z11=(1-(p/p0)^((R*(T0-T11))/(g*z11)))/(1-T11/T0);z50kPa:=solve(subs(p=85.7e3,dat,SI0,%),z)*m_;

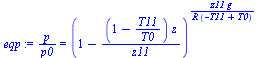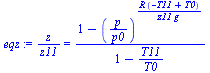En la estratosfera:

>	sol3_:=subs(p11=rhs(sol2_11),dat,sol3);for i from 11 to 20 by 1 do cat(p,i)=Pa_*Re(subs(z=i*1000,SI0,rhs(sol3_)));od;

>	plot([[z,rhs(subs(SI0,sol1_)),z=0..-1e3],[z,rhs(subs(SI0,sol2_)),z=0..11e3],[z,rhs(subs(SI0,sol3_)),z=11e3..20e3]],z=-1e3..20e3,p=0..2e6);

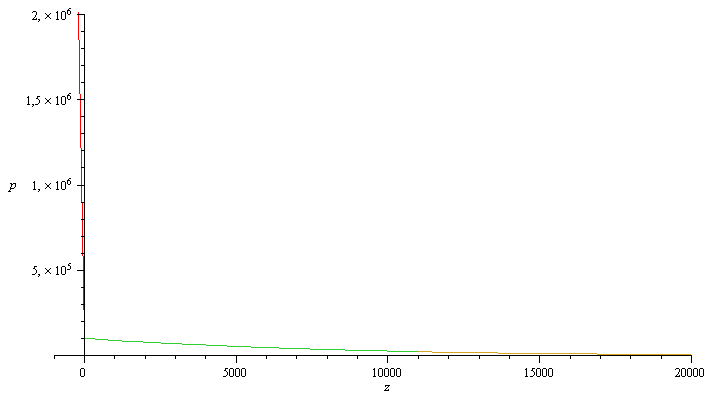Altitud a la que la presión es la mitad de la del nivel del mar.

>	eqz;z50kPa:=solve(subs(p=50e3,dat,SI0,eqz),z)*m_;

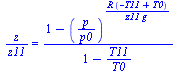Variación de g con h:

>	eqG:=F=G*m*M/d^2;eqg:=F=m*g;sol4:=solve(rhs(eqG)/rhs(eqg)=1);g10km:=subs(sol4,d=R[T]+10e3*m_,dat,g):g0:=subs(sol4,d=R[T],dat,g):'g10km/g0'=evalf(g10km/g0,3);g500km:=subs(sol4,d=R[T]+500e3*m_,dat,g):'g500km/g0'=evalf((g500km/g0),3);

b) El estado descrito ¿es de equilibrio, o meramente estacionario? ¿Cómo se interpreta que el perfil de temperatura tenga un máximo local a nivel del mar, a la luz de la transmisión de calor y el balance energético?

Es estacionario, pero no es estado de equilibrio termodinámico, pues la superficie terrestre se comporta como un generador de calor debido a la absorción de la radiación solar.

c) ¿Qué espesor de hidrosfera tiene la misma capacidad térmica que toda la atmósfera?

La masa de la atmósfera es de 1 kg/cm2, luego la masa de agua equivalente será de 1.1000/4200=0,24 kg/cm2, es decir, 2,4 m de profundidad, lo que explica que sean las corrientes marinas las que controlan el clima general de la tierra.

>	rho[aire0]:=evalf(subs(dat,dat,subs(p=p0,T=T0,rhs(eq1_12))),2);m_air_total:=p0*4*Pi*R[T]^2/g;m_air_total_:=subs(dat,evalf(%));h_air_rho0:=evalf(subs(dat,dat,p0/(g*rho[aire0])));h_water_mc_equiv:=evalf(h_air_rho0*rho[aire0]*subs(dat,dat,c[p]/(rho[0]*c)));

Pese a que 2,5 m de agua tienen la misma capacidad térmica que toda la atmósfera, para el transporte térmico influyen las velocidades.

d) Si el barómetro de un avión marca media atmósfera, ¿a qué altura vuela?

>	eqz;z50kPa:=solve(subs(p=50e3,dat,SI0,eqz),z)*m_;

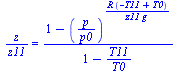Unos 5,5 km. Como las variaciones meteorológicas de la presión son pequeñas, mucho menores que las de temperatura, el barómetro sirve de altímetro aproximado.

>